Latency-Optimized Topology

A network’s topology, the structural design of how nodes interconnect, is a key aspect in optimizing network performance. Fleek Network employs a sophisticated, latency-focused, hierarchical clustering methodology in its approach to building an effective topology. This technique diverges from traditional reliance on geographic coordinates, opting instead for latency measurements to guide cluster formation.

This method facilitates efficient message propagation and ensures stability across the network. To arrive at this method method, there were a number of set-ups considered by Fleek Network’s core developers, across the clustering algorithm, hierarchical approaches, and pairing algorithms.

TLDR:

• Fleek Network's topology is structured using a latency-focused, hierarchical clustering methodology, diverging from traditional geographic-based systems.
• The network's clustering algorithm integrates principles from Constrained K-Means and FasterPAM, forming clusters of equal size based on latency measurements.
• Hierarchical structuring is achieved through a top-down approach, optimizing for minimal latency within clusters and efficient message propagation.
• A novel Heuristic Greedy pairing algorithm connects clusters, prioritizing low-latency connections for rapid message dissemination.
• Testnet results demonstrate the effectiveness of this approach, showing reduced latency and improved network performance compared to traditional methods.

The ensuing article explores the specific algorithms and strategies used to achieve Fleek Network's topology, providing insights into the core developers' methodologies and the technical intricacies of the network’s design:

Motivation

In peer-to-peer networks, nodes typically form an overlay network on top of the IP layer. The network's requirements highly influence the choice of the overlay network’s topology. There are many properties to consider, including but not limited to robustness, efficiency, and speed. Some of these properties are in direct competition with each other. For example, a robust network is the goal, where every node is guaranteed to receive broadcast messages from its peers, even in the face of network churn (nodes going on and offline). This could be achieved by choosing a topology for the overlay network that facilitates many redundant peer connections. However, this network will not be efficient because peers are likely to receive the same message several times, producing a lot of unnecessary communication between nodes.

To strike a trade-off between these properties, a clustering-based approach is used, along with forming several hierarchical layers, each containing more and more nodes up the tree. At each layer, a node is connected to at least one node in every other cluster. The clusters are formed through latency measurements, ensuring that once a single peer receives a message, the rest of the cluster will receive it quickly due to the low latency within the cluster. This approach minimizes the number of necessary connections and messages needed such that if any node fails to receive a message, another node in its cluster would be able to share it instead. This also keeps a level of redundancy, since each node inside a single cluster has its own unique connections to all other clusters.

These clusters also offer benefits beyond message propagation, such as being able to do small-scale “local” consensus for computations, where it ensures that latency is not a huge limiting factor. Additionally, they can be leveraged for replicating cached content to nodes in a similar area.

Overview

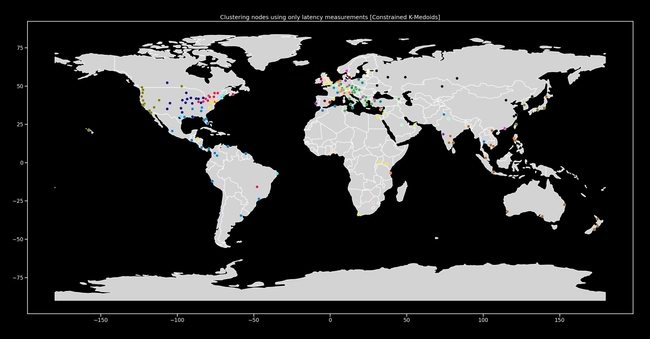
Figure 1: An example clustering of nodes based on latency, plotted on a map.

There is a very specific set of requirements for the clustering that dictates the novel solution: the algorithm should be deterministic, clusters should be all around the same size, the algorithm should be resilient to noisy data in the event of bad actors or missing values, and connection pairings should be redundant enough to ensure network churn does not leave any nodes orphaned from broadcasted messages. Keep in mind the network does not have an inherent understanding of geography but rather collects latency information over time and uses that to find a suitable clustering for a given epoch.

The current clustering algorithm integrates principles from Constrained K-Means [1], FasterPAM [2] (a K-Medoids algorithm), a top-down solution to form a hierarchy, and a novel pairing solution to connect clusters together. At each layer of this hierarchy, the clusters are interconnected by greedily pairing nodes based on their latency, preferring a few optimal connections between the clusters, rather than a good average latency between all pairings. This is acceptable since, at the final clusters, every node is directly connected to the nodes in its cluster, and can propagate a message very quickly instead of relying on other clusters to give messages.

The clustering algorithm is composed of the following steps:

• Find an optimal N number of central nodes, also known as medoids, in the network using the FasterPAM [1] algorithm
• Formulate and solve a min-cost-flow graph problem similar to the Constrained K-Means algorithm, assigning nodes to their optimal centers established by the previous step while ensuring that each cluster has around the same target number of nodes.
• Greedily pair each node between the resulting clusters based on their latencies.
• For each resulting cluster, step 1 is repeated until the resulting clusters contain approximately the desired number of nodes. For the last level of the hierarchy, the N number of clusters produced can be less than the starting N for the last clustering, to get approximately the target number of nodes per final cluster.

The full algorithm’s reference implementation is available here.

Clustering Algorithms

We explored several clustering algorithms to find one that suits the network’s requirements. While popular, the K-Means algorithm requires Euclidean coordinates to compare distances, and the clusters it produces may be of different sizes. Another algorithm, Constrained K-Means [1], addresses one of these issues by employing a minimum-cost-flow-graph (solved via the network simplex algorithm, the implementation uses the LEMON graph optimization library [4]) to ensure the clusters contain approximately a target number of nodes. The other significant issue is that geographical coordinates for distance is not used. Instead, latency information is used as distances, which these algorithms cannot use directly. K-Medoids (specifically the FasterPAM [2] algorithm) uses embeddings of “distances” instead of coordinates to find the clusters, which allows for the use the latency information directly. The concepts of the minimum cost flow graph from the constrained algorithm, along with the centers of the network found through K-Medoids, can then combine to get a unique clustering algorithm that uses latency information and produces clusters of equal sizes.

Hierarchical Approaches

Two approaches were evaluated to form the hierarchy of nodes: building the hierarchy from the bottom-up and building it from the top-down. The bottom-up approach entails clustering the nodes for the lowest level first and then repeatedly clustering the clusters from the previous level. For the top-down approach, the process starts at the highest level and recursively clusters the nodes within each cluster to form the clusters for the lower levels.

Bottom Up (Agglomerative)

The process begins by clustering the nodes in the network using the constrained algorithm. Each node is greedily connected to the closest node in every other cluster, where closeness is defined using the latency between nodes. Each cluster is then represented by its medoid, and both the clustering and greedy pairings are repeated with the medoids to form the clusters for the next level. This process is repeated until only two clusters remain.

Top Down (Divisive)

Starting at the hierarchy’s top level, eight clusters form at each division until the lowest level. The lowest level of the hierarchy might have a different number of clusters, depending on the specified cluster size. Starting at the top level, the nodes are clustered using the constrained algorithm and then greedily paired together. The nodes within each cluster are then clustered again to form the lower-level clusters. This division happens recursively until the stopping condition is satisfied, which is that the resulting clusters would have less than the target number of nodes.

Comparison

During simulations, the bottom-up strategy was not able to minimize latency within the clusters as well, while also taking an order of magnitude more time to run for a network of 20,000 nodes. The top-down approach is much faster, easily parallelizable if needed, and produces coherent clusters with better overall latency between nodes in the final clusters. Most of the speed benefits of the top-down approach are due to chunking up the time complexity of each step, iteratively processing fewer and fewer nodes at a time.

Pairing Algorithms

As mentioned above, after clustering the nodes, every cluster must connect to every other cluster. This is necessary to allow information to flow across the whole network of nodes, not just within each cluster. To connect two clusters (C1 and C2) with each other, every node in C1 must be connected to at least one node in C2, and vice versa. These pairings should be formed in a way that minimizes the latency across all node pairings. This task can be reduced to an assignment problem, where the bipartite graph can be represented by the matrix of pairwise latencies between nodes. A few pairing approaches were explored to solve this problem, two of which are outlined in the following sections.

Hungarian Algorithm

The Hungarian algorithm [3] solves the assignment problem in O(n³) time. This is not ideal because it can be computationally expensive for a large number of nodes. This approach also might forgo a few very optimal pairings, in an attempt to minimize the total latency between pairings, which is not ideal for propagating messages quickly.

Heuristic Greedy Pairing Algorithm

Due to the complexity of the Hungarian algorithm, a novel approach was devised. This algorithm prioritizes a few very fast connections, while others may be sub-optimal. This is acceptable since each end of the faster pairs between clusters can quickly propagate messages to their direct peers, which are optimized for latency by the clustering.

The pairing strategy is greedy, meaning that as each node is paired, it is removed from the list of possible options for the next node to pair with. The algorithm starts by sorting the nodes inside each cluster by a heuristic, which is the sum of their latency to nodes in the other cluster. This way, as each node is greedily paired with the node in the other cluster by the lowest latency, the nodes with the lowest sum of latencies have the most options to select from. In the event of two unequally sized clusters, the larger cluster is chunked such that the nodes with multiple connections to the other cluster have the lowest latency sums, and thus have the most options to pick from greedily.

Testnet Results

During the last testnet phase, latency measurements between nodes were collected to evaluate the clustering approach. As a baseline, clusters were formed randomly without taking into consideration any latency measurements. Figure 2 shows the median latency within all clusters for both the random baseline and the latency-informed clusters.

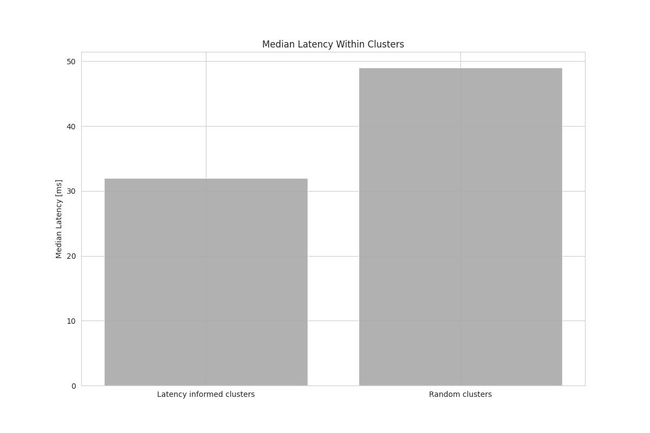Figure 2: Bar chart of median latencies within clusters

Figures 3 and 4 show a histogram of the pairwise latencies within clusters for both the random baseline and the clustering approach.

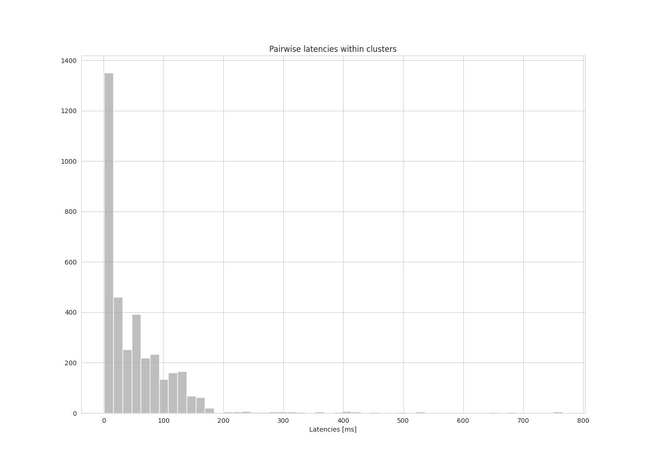Figure 3: histogram of pairwise latencies

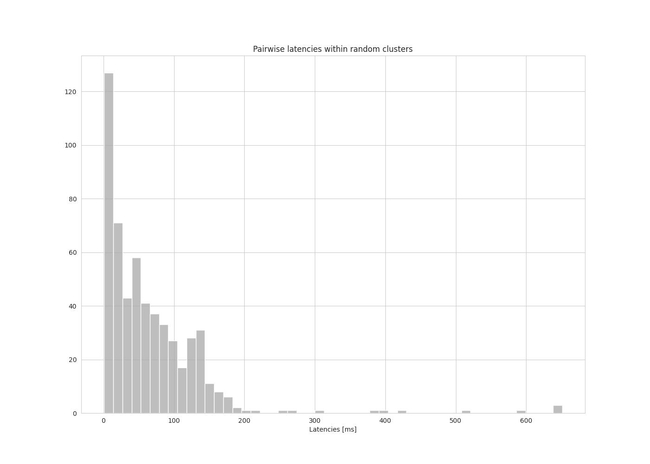Figure 4: histogram of pairwise latencies (random baseline)

Acknowledgments

Data made available by WonderProxy [5] was utilized in the above research and experiments. The dataset includes 250 servers, their geographical locations, and the pairwise latencies between them. Figure 1 (the map of the earth with the clustered servers) shows a map of servers. The servers were clustered purely based on latency using this approach. No geographical information was used to inform the clustering.

References

[1] P. S. Bradley, K. P. Bennett, and A. Demiriz. Constrained K-Means Clustering. Microsoft Research, Redmond 1-8, 2000. https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2000-65.pdf

[2] E. Schubert and P. J. Rousseeu. Fast and eager k-medoids clustering: runtime improvement of the PAM, CLARA, and CLARANS algorithms. Information Systems 101, 2021. https://www.sciencedirect.com/science/article/pii/S0306437921000557

[3] H. W. Kuhn. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly 2(1-2), pp. 83-97, 1955. https://onlinelibrary.wiley.com/doi/abs/10.1002/nav.3800020109

[4] B. Dezső, A. Jüttner, and P. Kovács. LEMON – an Open Source C++ Graph Template Library. Electronic Notes in Theoretical Computer Science, 264(5), pp. 23-45, 2011. https://www.sciencedirect.com/science/article/pii/S1571066111000740

[5] WonderProxy Dataset: https://wonderproxy.com/blog/a-day-in-the-life-of-the-internet/