Leveraging Narwhal & Bullshark For Consensus To Meet The High Demands Of An Edge Network

All nodes on Fleek Network have the same succinct state. This state includes information about account balances, work performed by nodes, reputation scores, and more. In order to achieve state machine replication, all nodes start from the same state (also called the genesis), and then continuously apply the same state transition functions in the same order. The mechanism that ensures that all valid nodes undergo the same state transitions, even in the presence of malicious (Byzantine) nodes, is called consensus.

Consensus mechanisms in distributed systems have been researched for decades, but have garnered more attention in the last couple of years, due to the emergence of blockchains.

A key metric that a variety of research in this area aims to improve is throughput. Throughput is often measured by how many state transition functions (or transactions) can be applied per second. For example, Bitcoin clocks in at around seven transactions per second. When a node on the Bitcoin network receives a transaction from a client, it will broadcast the transaction to the other nodes. These pending transactions are first verified and then stored on the nodes. The storage for these transactions is called the mempool. Miners on the network will periodically take transactions from the mempool and bundle them into a block. The miner that wins the proof of work race gets to propose its block to extend the current chain. The miner will then broadcast the block to the entire network.

One key observation here is that a transaction is broadcasted over the network twice; once through the mempool protocol and then again when the block is added to the chain.

DAG-based Mempools and Narwhal

Recent work [1, 2, 3] has proposed a new class of mempool protocols, in order to increase consensus throughput. The work is based on a key idea: transaction dissemination should be separated from the consensus protocol. This means that the transaction dissemination should not be handled by the consensus mechanism, which should solely be responsible for ordering transactions. Outsourcing the dissemination of transactions to the mempool protocol ensures that it is no longer on the critical path of transaction ordering, because it can happen in parallel.

The culmination of this line of research is the Narwhal system [3], which assumes that there are n validators that can communicate over a network. Up to f may be Byzantine faulty, where f < n/3. Furthermore, message delays between validators may be unbounded, and a finite but an unknown number of messages may be lost. The Narwhal system is based on rounds. In each round, each honest validator will propose one block. A block contains information about transactions as well as references to at least n - f blocks from the previous round. Crucially, a block doesn't contain the transactions themselves, but rather the transaction hashes (digests), together with a proof of availability that guarantees that the transactions will be available to download. This keeps the blocks small in size and limits the networking overhead. A validator can move to the next round, once it has seen n - f blocks from other validators in the current round. The blocks for each round together with the references to blocks from previous rounds form a directed acyclic graph (DAG), see Fig. 1. For more details about Narwhal, we refer to the excellent original work [3].

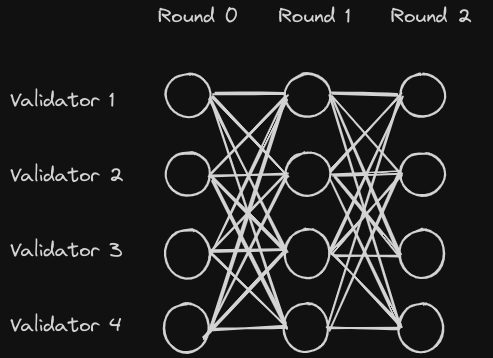
Figure 1: The DAG structure of blocks proposed by validators in the Narwhal system.

Transaction Ordering and Bullshark

Once the DAG is constructed as explained in the previous section, the blocks in the DAG have to be ordered to ensure that all validators execute the same transactions in the same order. The consensus engine on Fleek Network relies on Bullshark [4, 5] for this. Notably, Bullshark can achieve this without any networking overhead. Each validator uses its local DAG and is able to order the blocks without any additional communication with other validators.

Every even-numbered round in the DAG has a leader. In the simplest case, this leader can be determined through a round-robin. The block associated with the leader is called an anchor. The validators have to collectively agree on which anchors to order, and which anchors to skip. This is achieved by interpreting the references from the blocks in the odd-numbered rounds as votes. Specifically, if block A in round r has a reference to block B in round r - 1, then block A contributes one vote to block B. An anchor will be committed if it receives f + 1 votes. Once an anchor is committed, the blocks it references from previous rounds (and the blocks they reference) are ordered by some deterministic rule.

Due to networking delays, it is possible that at any point in time, two validators have a different local view of the DAG. For example, validator 1 in Fig. 2 already received anchor A from validator 4, while validator 3 did not. Validator 1 sees that anchor A has received enough votes (highlighted in red) and therefore commits it. To ensure the total ordering of blocks, validator 3 has to commit anchor A before it commits anchor B, even though it has not seen A yet. This is guaranteed by quorum intersection. An anchor is only committed if it has f + 1 votes, and each

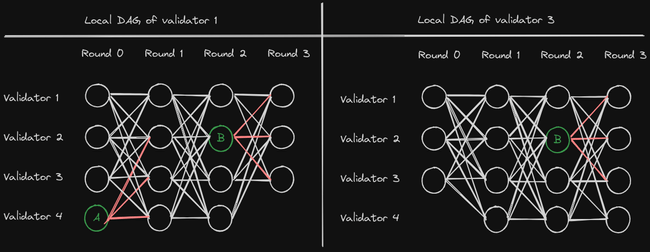Figure 2: Local DAGs from the perspective of two different validators. The green blocks in even-numbered rounds are the anchors. The votes from blocks in odd-numbered rounds are highlighted in red.

block has at least n - f references to blocks in the previous round. Thus, if a validator commits an anchor A, then all anchors in the following rounds must have a path (a chain of references) to at least one block that voted for A, and therefore will have a path to A. To see why this always holds, consider an anchor A in round r - 1 that receives f + 1 votes from blocks in round r, and will therefore be committed. Let's assume for the sake of contradiction that there is an anchor B in round r + 1 that does not have a path to anchor A. There are at least f + 1 blocks in round r that have a reference to anchor A (otherwise A would not have been committed). Since anchor B cannot have a path to anchor A, it cannot have a reference to any of these f + 1 blocks in round r. However, in order to be a valid block, anchor B must have at least n - f references to the blocks in round r. But there are at most n - f - 1 blocks in round r without a reference to anchor A, a contradiction. This means that the only scenario where there is no path from anchor B to anchor A is if anchor A did not receive enough votes and therefore no honest validator committed it. In that case it is safe and even necessary to skip anchor A entirely.

Going back to the example in Fig. 2, where validator 1 already received anchor A, and validator 3 did not. In round 1, validator 1 will see that anchor A has enough votes and will therefore commit it. Validator 3 won’t commit anchor A in round 1, because it hasn’t received it yet. However, once validator 3 commits anchor B in round 3, it will order the causal history of B, which includes anchor A. This illustrates that different local views of the DAG cannot lead to a different order of blocks. It can only lead to blocks being committed in different rounds, which is completely safe. For more details about Bullshark, we refer to [4, 5].

Consensus and Committees

The consensus protocol explained in the previous sections (specifically Narwhal and Bullshark) is only executed by a subset of nodes on Fleek Network at a particular point in time. This subset of nodes is referred to as the committee and changes every epoch. Committee-based protocols are necessary to achieve consensus with lower latency and higher throughput.

In the following, a node that is part of the committee in a particular epoch will be called a validator. A node that is not a validator in a particular epoch will be called a non-validator. While non-validators do not participate in the consensus protocol, they still need to execute the same transactions in the same order as the validators. This could easily be achieved by using a total order broadcast. However, the purpose of using a committee-based consensus protocol is to increase throughput and lower latency. The complexity of a total order broadcast would defeat that purpose.

Instead, the nodes on Fleek Network communicate over a best-effort broadcast that is based on the QUIC protocol. Note that while QUIC is a reliable transport protocol, the state between two parties is lost if the connection drops, and thus re-transmission of lost messages does not extend beyond the lifetime of a connection. Therefore, the best-effort broadcast is using a reliable transport protocol, but is itself not a reliable broadcast. This ensures that the dissemination of transactions to non-validators does not become a bottleneck for the consensus. The nodes on Fleek Network use a latency-informed, hierarchical clustering method to form the topology that underpins the broadcast. To learn how this facilitates efficient message propagation and ensures stability across the network, see this blog post: https://blog.fleek.network/post/latency-optimized-topology/.

The next section explains how the total order of transactions that is derived from the consensus protocol is communicated to non-validators, and how a best-effort broadcast can be used for this, without lowering the security guarantees of the overall consensus protocol.

Transaction Ordering for Non-Validators

The consensus protocol running on validators will continuously output ordered transactions that can be executed. Validators will execute these transactions, then group them into so-called parcels, and broadcast them to the non-validators. In addition to parcels, each validator will also broadcast an attestation for each parcel, which cryptographically proves that the validator has verified and executed the transactions in the parcel. Non-validators will only execute the transactions in a given parcel if they received 2f + 1 attestations for that particular parcel. This is necessary in order to uphold the security assumptions made by Narwhal and Bullshark. If a non-validator executes a parcel without receiving a quorum of attestations, then a minority of Byzantine validators could cause a fork.

Since the broadcast does not impose a total order on the messages, non-validators cannot simply execute a parcel, even if they received 2f + 1 attestations for it. Instead, each parcel contains a reference to the previous parcel. Non-validators keep track of the last parcel they executed, and only execute a new parcel if it points to this last executed parcel.

The structure of this chain of parcels affords an optimization that allows non-validators to execute parcels without 2f + 1 attestations, in certain cases. Consider the parcel chain in Fig. 4. Parcels 0 and 1 have already been executed. Parcels 2, 3, and 4 haven’t received 2f + 1 attestations yet. However, parcel 5 has received at least 2f + 1 attestations. In this case it is completely safe to execute parcels 2, 3, 4, and 5. The reason is that parcel 5 has received at least 2f + 1 attestations and is therefore safe to execute. Since parcel 5 points to parcel 4, it is also safe to execute parcel 4. Every validator that executed parcel 5, also executed parcel 4. The same argument can be applied inductively to parcels 3 and 2.

Figure 4: A chain of parcels. The dashed parcels haven’t received 2f + 1 attestations yet.

Recovering Lost Broadcast Messages

Since the broadcast is not a reliable broadcast, messages can be lost. This happens infrequently but has to be dealt with nonetheless. Recall how non-validators build up a chain of parcels, in order to preserve the transaction ordering imposed by the consensus protocol. A parcel can only be executed if it received enough attestations, and if it points to the last executed parcel. Fig. 3 shows an example where a non-validator executed parcels 0, 1, and 2, and already received parcel 4. Parcel 3 was either lost or is arriving out of order. If parcel 3 simply arrives out of order, everything still works as expected. Once parcel 3 arrives with enough attestations, it will be executed, since it points to the last executed parcel. Once enough attestations are received for parcel 4, it can be executed as well. However, if parcel 3 was in fact lost, the non-validator could never execute another parcel again without violating the ordering of transactions. To prevent this, non-validators can send a message to other nodes on Fleek Network to request a missing parcel. This message will only be sent after a certain time has passed in order to prevent a premature parcel request for a parcel that is arriving out of order.

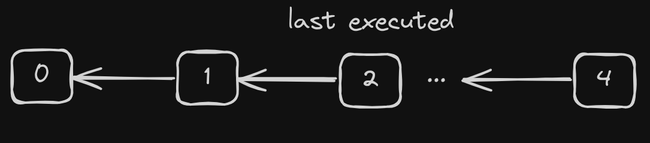Figure 3: A chain of parcels that is constructed on a non-validator. Parcel 2 is the last executed parcel, and parcel 3 is either missing or arrives out-of-order. Parcel 4 can only be executed after parcel 3.

Future Work

As explained above, Bullshark defines a mapping over the validators that selects a leader for each even round whose block will become the anchor. If the anchor receives f + 1 votes, it will be committed. However, if the leader for a given round is slow or unresponsive, its associated anchor cannot be committed. Uncommitted anchors increase the latency of the consensus protocol.

Recent work [5] proposes to improve the latency of DAG-based consensus protocols, such as Narwhal and Bullshark, by incorporating validator reputation. Specifically, the mapping that defines the leader will take the validator’s reputation into consideration.

All nodes on Fleek Network have a reputation score that aggregates several properties such as a node’s uptime. If a node’s uptime falls below a certain threshold, the node won’t be able to participate in the following epoch. This aims to ensure the availability and responsiveness of the network and prevent unanswered requests from clients.

To incorporate some of the ideas from [5] into Fleek Network’s consensus engine, a second (higher) threshold for node uptime could be introduced and only nodes that satisfy this threshold will be eligible for the consensus committee.

References

[1] Adam Gkagol, Damian Lesniak, Damian Straszak, and Michal Swiketek. Aleph: Efficient atomic broadcast in asynchronous networks with Byzantine nodes. In Proceedings of the 1st ACM Conference on Advances in Financial Tech- nologies. 214–228, 2019.

[2] Idit Keidar, Eleftherios Kokoris-Kogias, Oded Naor, and Alexander Spiegelman. All You Need is DAG. In Proceedings of the 40th Symposium on Principles of Distributed Computing (PODC ’21). Association for Computing Machinery, New York, NY, USA, 2021.

[3] George Danezis, Lefteris Kokoris-Kogias, Alberto Sonnino, and Alexan- der Spiegelman. Narwhal and tusk: a dag-based mempool and efficient bft consensus. In Proceedings of the Seventeenth European Conference on Computer Systems. 34–50, 2022.

[4] Alexander Spiegelman, Neil Giridharan, Alberto Sonnino, and Lefteris Kokoris-Kogias. Bullshark: Dag bft protocols made practical. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 2705–2718, 2022.

[5] Alexander Spiegelman, Neil Giridharan, Alberto Sonnino, and Lefteris Kokoris-Kogias. Bullshark: The Partially Synchronous Version. arXiv preprint arXiv:2209.05633, 2022.

[6] Alexander Spiegelman, Balaji Arun, Rati Gelashvili, Zekun Li. Bullshark: The Partially Synchronous Version. arXiv preprint arXiv:2306.03058, 2023.